2022 수능 예시문항 문제 및 정답 다운로드(평가원)open in new window
21번 평가 난이도 : ★★☆☆☆ (2/5, 하)다루는 개념 : 사인법칙 코사인법칙
"기본 개념을 적용할 줄 아는지 확인하는 문제"
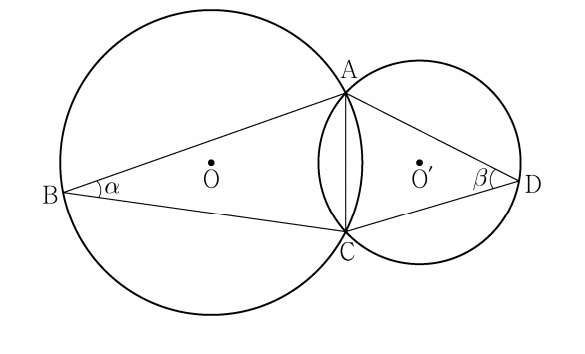
문제 그림과 같이 한 평면 위에 있는 두 삼각형 △ A B C \triangle ABC △ A B C △ A C D \triangle ACD △ A C D O O O O ′ O' O ′ ∠ A B C = α , ∠ A D C = β \angle ABC=\alpha, \angle ADC = \beta ∠ A B C = α , ∠ A D C = β
sin β sin α = 3 2 , cos ( α + β ) = 1 3 , O O ′ ‾ = 1 \frac{\sin\beta}{\sin\alpha}=\frac{3}{2}, \cos(\alpha+\beta)=\frac{1}{3}, \overline{OO'}=1 sin α sin β = 2 3 , cos ( α + β ) = 3 1 , O O ′ = 1
이 성립한다. △ A B C \triangle ABC △ A B C q p π \frac{q}{p}\pi p q π p + q p+q p + q
풀이 step1) 두 원의 반지름 비율 구하기
원O O O r r r O ′ O' O ′ r ′ r' r ′
△ A B C \triangle ABC △ A B C △ A D C \triangle ADC △ A D C 사인법칙에 의해,
A C ‾ sin α = 2 r , A C ‾ sin β = 2 r ′ \frac{\overline{AC}}{\sin \alpha}=2r, \frac{\overline{AC}}{\sin \beta}=2r' sin α A C = 2 r , sin β A C = 2 r ′
이다.
따라서, r sin α = r ′ sin β r\sin\alpha =r'\sin\beta r sin α = r ′ sin β r : r ′ = 3 : 2 {\color{#5D7FE8} {r:r'=3:2} } r : r ′ = 3 : 2 ( ∵ sin β sin α = 3 2 ) (\because \frac{\sin \beta}{\sin \alpha}=\frac{3}{2}) ( ∵ sin α sin β = 2 3 )
step2) r값 구하기
△ A O O ′ \triangle AOO' △ A O O ′ 코사인법칙에 의해,
O O ′ ‾ 2 = O A ‾ 2 + O ′ A ‾ 2 − 2 O A ‾ ⋅ O ′ A ‾ ⋅ cos { π − ( α + β ) } \overline{OO'}^2=\overline{OA}^2+\overline{O'A}^2-2\overline{OA}\cdot \overline{O'A}\cdot \cos\{\pi-(\alpha+\beta)\} O O ′ 2 = O A 2 + O ′ A 2 − 2 O A ⋅ O ′ A ⋅ cos { π − ( α + β ) }
( 1 ) 2 = r 2 + ( r ′ ) 2 − 2 r r ′ cos { π − ( α + β ) } ( ∵ O O ′ ‾ = 1 ) (1)^2=r^2+(r')^2-2rr'\cos\{\pi-(\alpha+\beta)\} (\because \overline{OO'}=1) ( 1 ) 2 = r 2 + ( r ′ ) 2 − 2 r r ′ cos { π − ( α + β ) } ( ∵ O O ′ = 1 ) 1 = r 2 + ( 2 3 r ) 2 − 2 r ( 2 3 r ) ( − 1 3 ) ( ∵ cos ( α + β ) = 1 3 ) 1=r^2+(\frac{2}{3}r)^2-2r(\frac{2}{3}r)(-\frac{1}{3}) (\because \cos (\alpha+\beta)=\frac{1}{3}) 1 = r 2 + ( 3 2 r ) 2 − 2 r ( 3 2 r ) ( − 3 1 ) ( ∵ cos ( α + β ) = 3 1 )
∴ 1 7 9 r 2 = 1 \therefore \frac{17}{9}r^2 = 1 ∴ 9 1 7 r 2 = 1 r 2 = 9 1 7 , r^2=\frac{9}{17}, r 2 = 1 7 9 , S = π ⋅ r 2 = 9 1 7 π S=\pi \cdot r^2 = \frac{9}{17} \pi S = π ⋅ r 2 = 1 7 9 π
정답 ∴ p + q = 1 7 + 9 = 2 6 \therefore p+q = 17+9 = 26 ∴ p + q = 1 7 + 9 = 2 6
사용한 개념 사인법칙
△ A B C \triangle ABC △ A B C O O O
a sin A = b sin B = c sin C \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} sin A a = sin B b = sin C c
가 성립한다.
코사인법칙
피타고라스 정리의 일반화라고도 볼 수 있는 코사인 법칙이다:△ A B C \triangle ABC △ A B C
a 2 = b 2 + c 2 − 2 b c cos A a^2=b^2+c^2-2bc\cos A a 2 = b 2 + c 2 − 2 b c cos A
b 2 = c 2 + a 2 − 2 c a cos B b^2=c^2+a^2-2ca\cos B b 2 = c 2 + a 2 − 2 c a cos B
c 2 = a 2 + b 2 − 2 a b cos C c^2=a^2+b^2-2ab\cos C c 2 = a 2 + b 2 − 2 a b cos C
이다.
22번 평가 난이도 : ★★★☆☆ (3/5, 중)다루는 개념 : 다항함수의 미분 함수의 개형
"사용된 개념은 단순하고 쉬우나, 적용은 까다로운 문제"
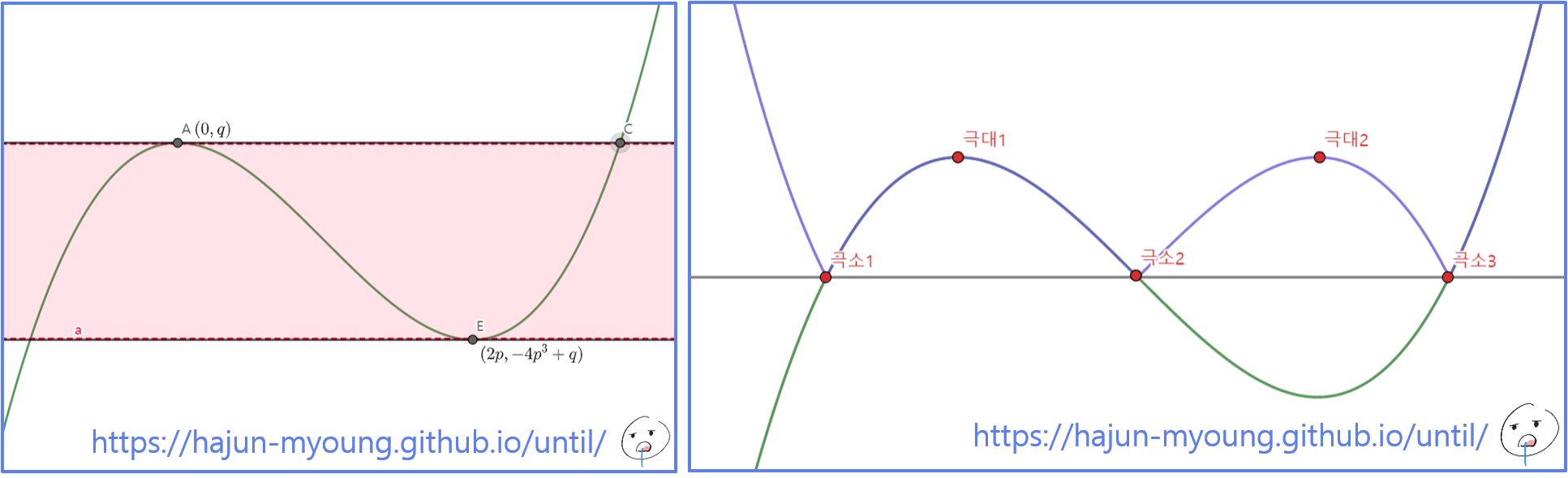
문제 함수 f ( x ) = x 3 − 3 p x 2 + q f(x)=x^3-3px^2+q f ( x ) = x 3 − 3 p x 2 + q p , q p, q p , q ( p , q ) (p, q) ( p , q )
(가) 함수 ∣ f ( x ) ∣ \vert f(x) \vert ∣ f ( x ) ∣ x = a x=a x = a a a a (나) 닫힌구간 [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] ∣ f ( x ) ∣ \vert f(x) \vert ∣ f ( x ) ∣ [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] ∣ f ( x ) ∣ \vert f(x) \vert ∣ f ( x ) ∣
풀이 step1) 조건 '가'를 해석해 p p p q q q
(left) 범위 a(빨간색)에 x축이 있어야 (right) ∣ f ( x ) ∣ \vert f(x) \vert ∣ f ( x ) ∣
d d x f ( x ) = 3 x 2 − 6 p x = 3 x ( x − 2 p ) \frac{d}{dx} f(x)=3x^2 -6px=3x(x-2p) d x d f ( x ) = 3 x 2 − 6 p x = 3 x ( x − 2 p ) f ( x ) f(x) f ( x ) x = 0 , 2 p x=0, 2p x = 0 , 2 p A ( 0 , q ) , B ( 2 p , − 4 p 3 + q ) A(0,q), B(2p, -4p^3+q) A ( 0 , q ) , B ( 2 p , − 4 p 3 + q )
− 4 p 3 + q < 0 < q -4p^3+q \lt 0 \lt q − 4 p 3 + q < 0 < q
이다. ( ∵ x (\because x ( ∵ x y = 0 ) y=0) y = 0 )
q q q 0 < q 0 \lt q 0 < q − 4 p 3 + q < 0 -4p^3+q \lt 0 − 4 p 3 + q < 0 q < 4 p 3 {\color{#5D7FE8} {q \lt 4p^3} } q < 4 p 3
step2) p p p
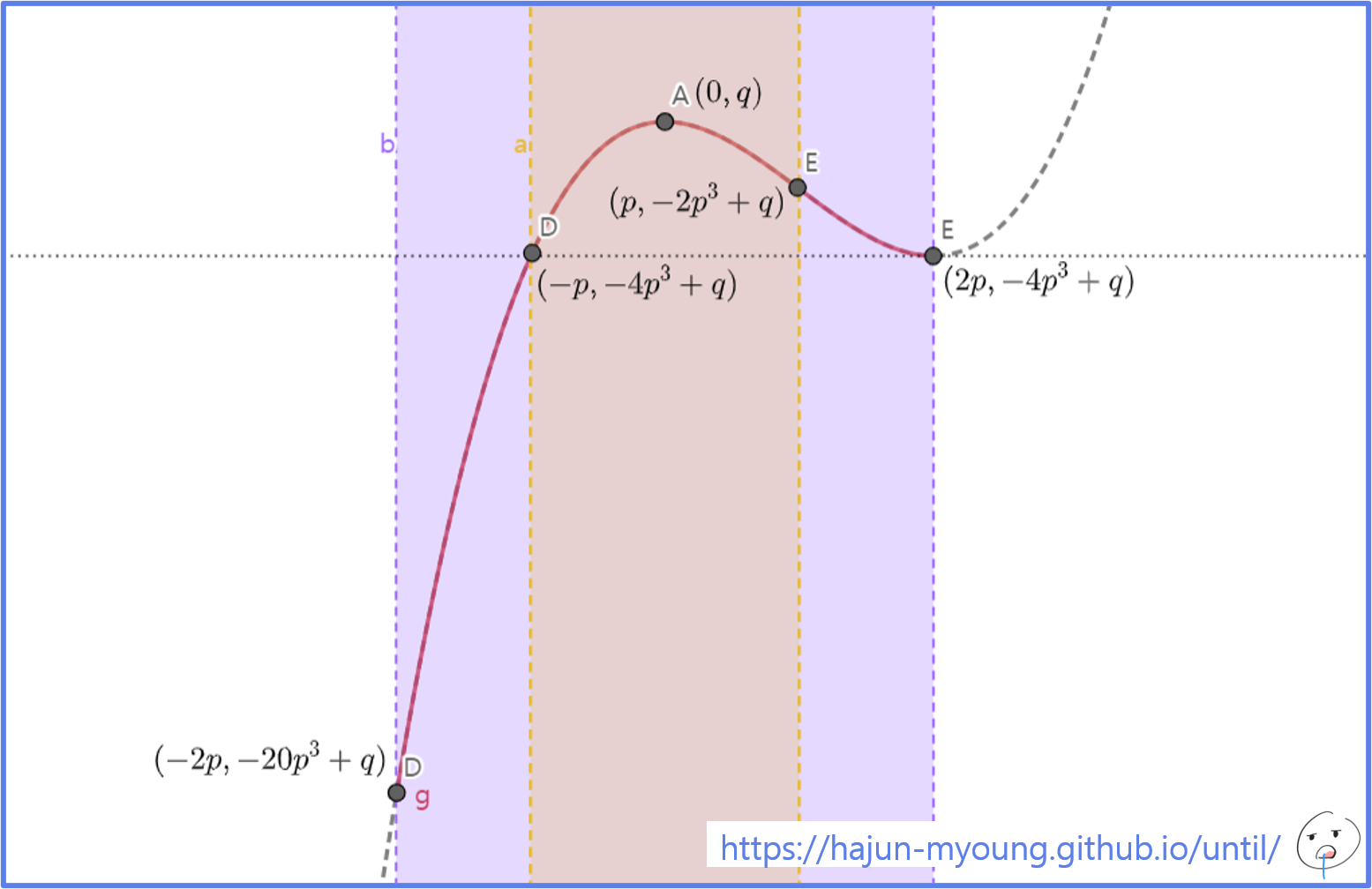
i ) p = 1 i)\ p=1 i ) p = 1 ∵ p , q ∈ \because p, q \in ∵ p , q ∈
닫힌구간 [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] [ − p , p ] [-p, p] [ − p , p ] 닫힌구간 [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] [ − 2 p , 2 p ] [-2p, 2p] [ − 2 p , 2 p ] [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] ∣ f ( x ) ∣ \vert f(x) \vert ∣ f ( x ) ∣ ∣ f ( − 1 ) ∣ = ∣ f ( − p ) ∣ = ∣ − 4 p 3 + q ∣ \vert f(-1) \vert = \vert f(-p) \vert = \vert -4p^3+q \vert ∣ f ( − 1 ) ∣ = ∣ f ( − p ) ∣ = ∣ − 4 p 3 + q ∣ [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] ∣ f ( x ) ∣ \vert f(x) \vert ∣ f ( x ) ∣ ∣ f ( − 2 ) ∣ = ∣ f ( − 2 p ) ∣ = ∣ − 2 0 p 3 + q ∣ \vert f(-2) \vert = \vert f(-2p) \vert = \vert -20p^3+q \vert ∣ f ( − 2 ) ∣ = ∣ f ( − 2 p ) ∣ = ∣ − 2 0 p 3 + q ∣
∣ − 4 p 3 + q ∣ < ∣ − 2 0 p 3 + q ∣ \vert -4p^3+q \vert < \vert -20p^3+q \vert ∣ − 4 p 3 + q ∣ < ∣ − 2 0 p 3 + q ∣
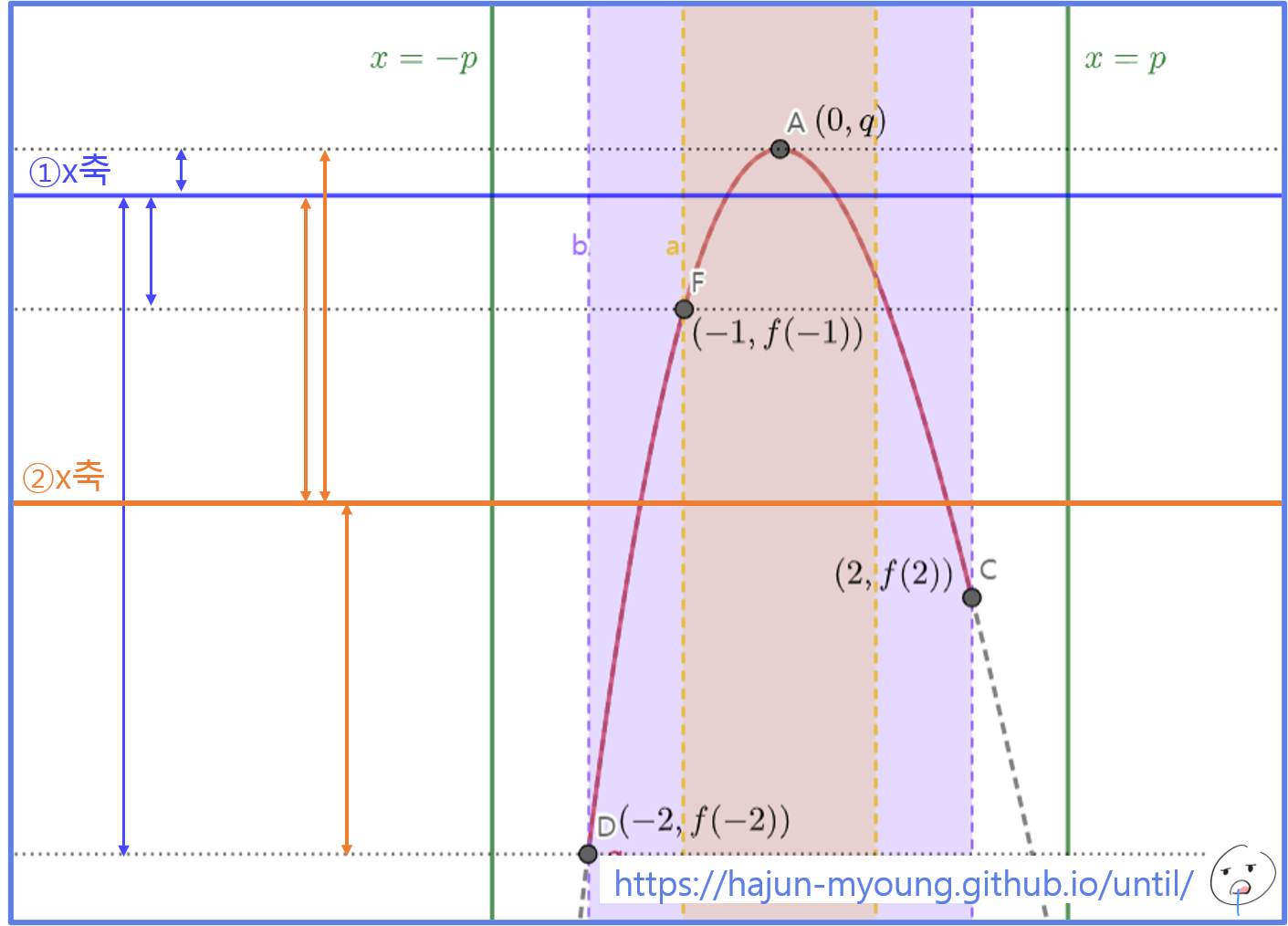
i i ) p ≥ 2 ii)\ p\ge 2 i i ) p ≥ 2
가장 큰 닫힌구간 [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] [ − p , p ] [-p, p] [ − p , p ]
① [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] ∣ f ( − 1 ) ∣ \vert f(-1) \vert ∣ f ( − 1 ) ∣ ∣ f ( − 2 ) ∣ > ∣ f ( − 1 ) ∣ \vert f(-2) \vert \gt \vert f(-1) \vert ∣ f ( − 2 ) ∣ > ∣ f ( − 1 ) ∣
② [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] f ( 0 ) f(0) f ( 0 ) [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] f ( 0 ) f(0) f ( 0 )
[ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] f ( 0 ) f(0) f ( 0 ) ∣ f ( 0 ) ∣ ≥ ∣ f ( − 1 ) ∣ \vert f(0) \vert \ge \vert f(-1) \vert ∣ f ( 0 ) ∣ ≥ ∣ f ( − 1 ) ∣ [ − 2 , 2 ] [-2, 2] [ − 2 , 2 ] f ( 0 ) f(0) f ( 0 ) ∣ f ( 0 ) ∣ ≥ ∣ f ( − 2 ) ∣ \vert f(0) \vert \ge \vert f(-2) \vert ∣ f ( 0 ) ∣ ≥ ∣ f ( − 2 ) ∣ ∣ f ( 0 ) ∣ ≥ ∣ f ( − 2 ) ∣ \vert f(0) \vert \ge \vert f(-2) \vert ∣ f ( 0 ) ∣ ≥ ∣ f ( − 2 ) ∣ ∣ f ( 0 ) ∣ ≥ ∣ f ( − 1 ) ∣ \vert f(0) \vert \ge \vert f(-1) \vert ∣ f ( 0 ) ∣ ≥ ∣ f ( − 1 ) ∣
f ( 0 ) ≥ − f ( − 2 ) f(0) \ge -f(-2) f ( 0 ) ≥ − f ( − 2 )
q ≥ 8 + 1 2 − q q \ge 8+12-q q ≥ 8 + 1 2 − q
q ≥ 4 + 6 p q \ge 4+6p q ≥ 4 + 6 p
step1에서의 결과와 종합하면, 4 + 6 p ≤ q < 4 p 3 {\color{#5D7FE8}{ 4+6p \le q \lt 4p^3 }} 4 + 6 p ≤ q < 4 p 3
정답 p = 2 , 1 6 ≤ q < 3 2 p=2,\ 16 \le q \lt 32 p = 2 , 1 6 ≤ q < 3 2 ∵ q ≤ 2 5 \because q \le 25 ∵ q ≤ 2 5 p = 3 , 2 2 ≤ q < 4 ⋅ 3 3 p=3,\ 22 \le q \lt 4 \cdot 3^3 p = 3 , 2 2 ≤ q < 4 ⋅ 3 3 p ≥ 4 , 2 8 ≤ q p\ge 4,\ 28 \le q p ≥ 4 , 2 8 ≤ q
따라서, 자연수 p , q p, q p , q ( p , q ) (p, q) ( p , q )
29번 평가 난이도 : ★★★★☆ (4/5, 상)다루는 개념 : 적분으로 정의된 함수 적분으로 정의된 함수의 미분 치환적분
"함수의 개형을 그리고, 순서에 맞게 '해석'하면 이해되는 문제"
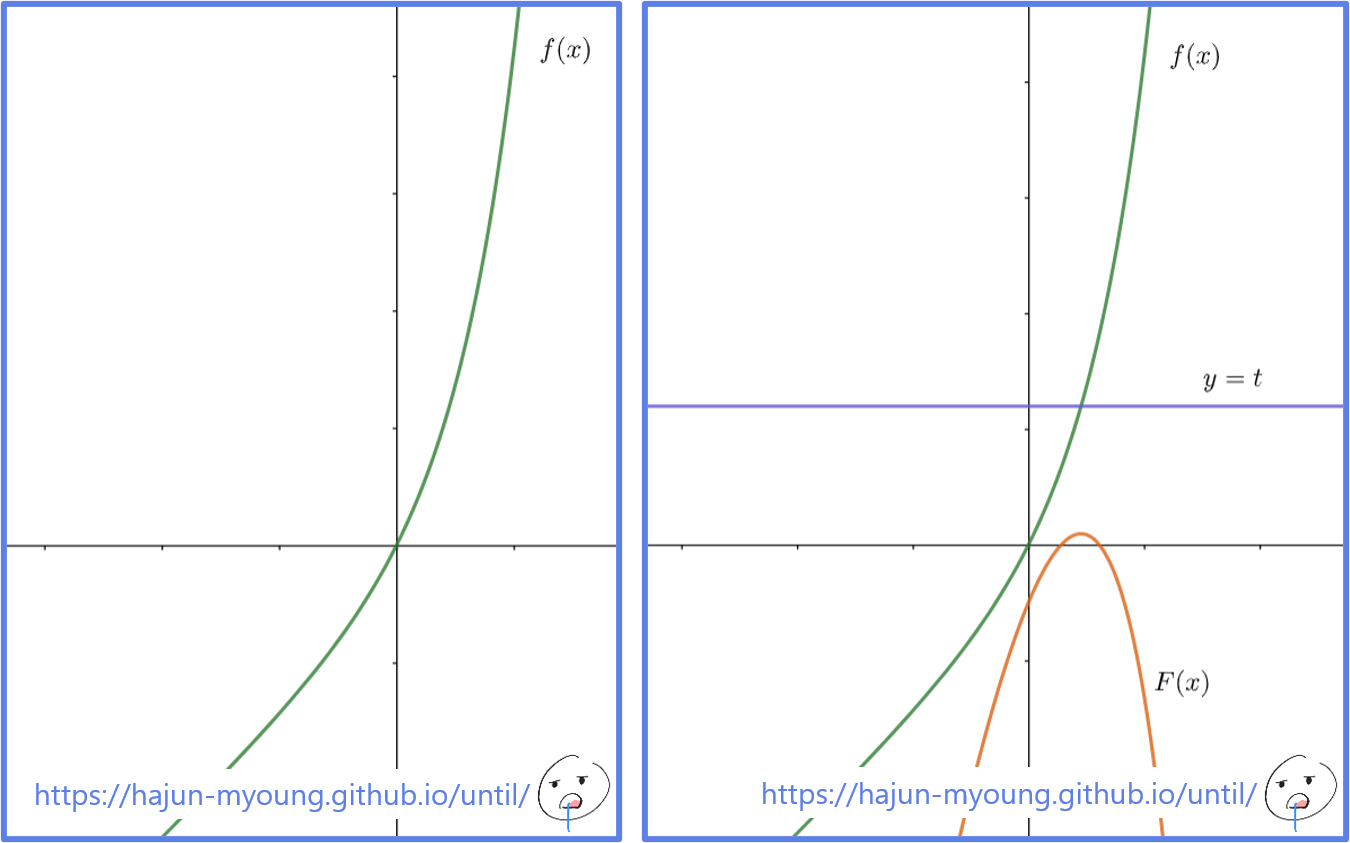
문제 함수 f ( x ) = e x + x − 1 f(x)=e^x +x-1 f ( x ) = e x + x − 1 t t t F ( x ) = ∫ 0 x { t − f ( s ) } d s F(x)=\int_{0}^{x} \{t-f(s)\}ds F ( x ) = ∫ 0 x { t − f ( s ) } d s x = α x=\alpha x = α α \alpha α g ( t ) g(t) g ( t ) g ( t ) g(t) g ( t ) ∫ f ( 1 ) f ( 5 ) g ( t ) 1 + e g ( t ) d t \int_{f(1)}^{f(5)} \frac{g(t)}{1+e^{g(t)}} dt ∫ f ( 1 ) f ( 5 ) 1 + e g ( t ) g ( t ) d t
풀이 step1) 함수 f ( x ) f(x) f ( x ) F ( x ) F(x) F ( x ) f ( x ) f(x) f ( x )
F ( x ) = ∫ 0 x { t − f ( s ) } d s F(x) = \int_{0}^{x} \{t-f(s)\}ds F ( x ) = ∫ 0 x { t − f ( s ) } d s
∴ d d x F ( x ) = t − f ( x ) \therefore \frac{d}{dx} F(x) = t-f(x) ∴ d x d F ( x ) = t − f ( x )
이고 (두 함수의 관계),
f ( x ) = e x + x − 1 , f(x)=e^x+x-1, f ( x ) = e x + x − 1 ,
d d x f ( x ) = e x + 1 > 0 \frac{d}{dx} f(x)=e^x+1 \gt 0 d x d f ( x ) = e x + 1 > 0
이므로, 함수 f ( x ) f(x) f ( x ) ( 0 , 0 ) (0,0) ( 0 , 0 )
step2) 함수 f ( x ) f(x) f ( x ) F ( x ) F(x) F ( x )
함수 f(x)의 개형 그리기 범위 방법 x ≥ 0 x\ge 0 x ≥ 0 ( 0 , 0 ) (0,0) ( 0 , 0 ) e x e^x e x x < 0 x\lt 0 x < 0 lim x → − ∞ e x = 0 \lim\limits_{x\rightarrow -\infty}{e^x}=0 x → − ∞ lim e x = 0 x − 1 x-1 x − 1
함수 f ( x ) f(x) f ( x ) F ( x ) F(x) F ( x )
F ( x ) = ∫ 0 x { t − f ( s ) } d s F(x) = \int_{0}^{x} \{t-f(s)\}ds F ( x ) = ∫ 0 x { t − f ( s ) } d s y = t y=t y = t f ( x ) f(x) f ( x ) f ( x ) < t f(x)\lt t f ( x ) < t f ( x ) > t f(x)\gt t f ( x ) > t
y = t y=t y = t y = f ( x ) y=f(x) y = f ( x ) F ( x ) F(x) F ( x ) α \alpha α f ( α ) = t f(\alpha)=t f ( α ) = t
f ( α ) = t , f(\alpha)=t, f ( α ) = t ,
α = g ( t ) = f − 1 ( t ) \alpha=g(t)=f^{-1}(t) α = g ( t ) = f − 1 ( t )
함수 g ( x ) g(x) g ( x ) f ( x ) f(x) f ( x )
정답 치환적분을 통해 답을 구한다.
∴ ∫ f ( 1 ) f ( 5 ) g ( t ) 1 + e g ( t ) d t \therefore \int_{f(1)}^{f(5)} \frac{g(t)}{1+e^{g(t)}} dt ∴ ∫ f ( 1 ) f ( 5 ) 1 + e g ( t ) g ( t ) d t
g ( t ) = k g(t)=k g ( t ) = k t = f ( k ) , d t = f ′ ( k ) d k t=f(k), dt=f'(k)dk t = f ( k ) , d t = f ′ ( k ) d k t : f ( 1 ) t: f(1) t : f ( 1 ) f ( 5 ) f(5) f ( 5 ) k : 1 k:1 k : 1 5 5 5
= ∫ 1 5 k 1 + e k f ′ ( k ) d k = \int_{1}^{5} \frac{k}{1+e^k}f'(k)dk = ∫ 1 5 1 + e k k f ′ ( k ) d k
f ′ ( k ) = e k + 1 f'(k)=e^k+1 f ′ ( k ) = e k + 1
= ∫ 1 5 k 1 + e k ( e k + 1 ) d k = ∫ 1 5 k d k = 1 2 = \int_{1}^{5} \frac{k}{1+e^k}(e^k+1)dk {\color{#5D7FE8}{\ = \int_{1}^{5} k dk = 12}} = ∫ 1 5 1 + e k k ( e k + 1 ) d k = ∫ 1 5 k d k = 1 2
사용한 개념 적분으로 정의된 함수
적분으로 정의된 함수는, 적분범위에 따라 해석방향이 달라진다.
적분범위가 상수이면, 적분값도 상수임에 주의한다. 적분범위가 미지수이면, 적분값도 미지수임에 주의한다. 적분으로 정의된 함수의 미분
F ( x ) F(x) F ( x ) f ( x ) f(x) f ( x )
∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_{a}^{b} f(x)dx = F(b)-F(a) ∫ a b f ( x ) d x = F ( b ) − F ( a )
이다.F ( a ) , F ( b ) F(a), F(b) F ( a ) , F ( b ) 0 0 0
따라서, 적분범위에 미지수가 포함된
g ( x ) = ∫ a x f ( x ) d x = F ( x ) − F ( a ) g(x)=\int_{a}^{x} f(x)dx = F(x)-F(a) g ( x ) = ∫ a x f ( x ) d x = F ( x ) − F ( a )
와 같은 경우에 대해서만
g ′ ( x ) = { F ( x ) − F ( a ) } ′ = f ( x ) − 0 = f ( x ) g'(x) = \{F(x)-F(a)\}' = f(x)-0 = f(x) g ′ ( x ) = { F ( x ) − F ( a ) } ′ = f ( x ) − 0 = f ( x )
일 수 있다.
치환적분
∫ f ( g ( x ) ) g ′ ( x ) d x \int f(g(x))g'(x)dx ∫ f ( g ( x ) ) g ′ ( x ) d x
와 같은 꼴에 대해서, g ( x ) = t g(x)=t g ( x ) = t g ′ ( x ) d x = d t g'(x)dx=dt g ′ ( x ) d x = d t
∫ f ( t ) d t \int f(t)dt ∫ f ( t ) d t
로 계산할 수 있다.
만약 정적분인 경우, 적분변수가 x x x t t t
예를 들어,x x x a → b a \rightarrow b a → b t = g ( x ) t=g(x) t = g ( x ) g ( a ) → g ( b ) g(a) \rightarrow g(b) g ( a ) → g ( b )
30번(작성중) 평가 난이도 : ★★★★☆ (4/5, 상)다루는 개념 : lnx/x 꼴 함수의 개형 좌극한과 우극한
"주어진 조건들의 해석이 전부인 문제"
문제 두 양수 a , b ( b < 1 ) a, b (b<1) a , b ( b < 1 ) f ( x ) f(x) f ( x )
f ( x ) = { − x 2 + a x ( x ≤ 0 ) l n ( x + b ) x ( x > 0 ) f(x)=\left\{\begin{matrix} -x^2 + ax (x\leq 0) \\ \frac{ln(x+b)}{x} (x>0) \end{matrix}\right. f ( x ) = ⎩ ⎨ ⎧ − x 2 + a x ( x ≤ 0 ) x l n ( x + b ) ( x > 0 )
라고 하자.m m m y = m x y=mx y = m x y + f ( x ) y+f(x) y + f ( x ) g ( m ) g(m) g ( m ) g ( m ) g(m) g ( m )
lim m → α − g ( m ) − lim m → α + g ( m ) = 1 \lim\limits_{m\rightarrow\alpha -}g(m)-\lim\limits_{m\rightarrow\alpha +}g(m)= 1 m → α − lim g ( m ) − m → α + lim g ( m ) = 1 α \alpha α α \alpha α ( b , f ( b ) ) (b, f(b)) ( b , f ( b ) ) y = a x y=ax y = a x f ( x ) f(x) f ( x )
이 때, a b 2 = q p ab^2 = \frac{q}{p} a b 2 = p q p + q p+q p + q
풀이 정답 사용한 개념